데이터베이스 인덱스의 자료구조로 해쉬 테이블과 B+Tree 자료구조를 활용할 수 있다는 것을 알았다
추가로 범위 탐색에 용이한 B+Tree를 대부분 활용하며 리프노드에 선형 데이터를 담아놓아 메모리 효율성이나 데이터 탐색에 용이하다
B-Tree는 어디서 파생되었는지 B-Tree에서 왜 B+Tree가 나오게 되었고, 어떤 자료구조를 구현하여 효율적인 탐색이 가능해졌는지 정리해보고자 한다
이진트리
B-Tree도 트리 자료구조이며 깊이가 깊어지면 탐색의 비용이 커진다 이것은 트리 자료구조를 알면 어느 정도 이해가 될 것이다
이진트리의 탐색 비용은 얼마인가?

일반적인 이진트리는 편향 트리가 발생할 수 있어 탐색 비용은 O(N)이다
트리의 깊이가 깊어지면 비용이 올라간다는 말을 이해할 수 있을 것이다
탐색의 비용을 O(logN)을 보장하는 트리가 바로 균형 이진트리다(ex: AVL Tree, Red-Black Tree)
- 균형이진트리: leaf node들의 레벨차이가 최대 1 레벨까지만 나는 트리

균형을 유지하기 위한 비용을 지불하고, 탐색의 비용을 O(logN)을 보장하는 것
-> 쓰기 비용을 지불하고 조회 성능을 올리는 인덱스 사용 이유와 일치한다
이러한 이유에서 B-Tree는 균형이진트리에서 파생되었다
B-Tree, 균형이진트리 모두 average, worst 비용이 O(logN)인데
왜 균형이진트리가 아닌 B-Tree라는 새로운 자료구조를 만들어 사용하는지 알아보도록 하자
B-Tree (Balanced Tree)
B-Tree는 자식 2개 만을 갖는 이진트리(Binary Tree)를 확장하여 M개의 자식을 가질 수 있도록 고안된 것이다
또한 하나의 노드에 여러 정보를 담을 수 있고, 여러 자식을 가질 수 있게 되면서 차수라는 개념이 등장
차수와 관련된 B-Tree는 4가지 규칙이 있다
- 자식이 M개인 B-Tree를 M차 B-Tree라고 한다
차수인 M을 기준으로 설명하면
- M: 각 노드는 최대 M개의 자식 노드를 가질 수 있다
- M-1: 각 노드는 최대 M-1 개의 키를 가질 수 있다
- [M/2](올림): 각 노드는 최소 자녀를 [M/2] 개 가져야 한다(단, root node와 leaf node는 제외)
- 이진트리를 생각해 보면 중간 노드는 항상 2개의 자식 노드를 가진다 -> 1개의 키값에 2개의 자식
- [M/2](올림) - 1: 각 노드의 최소 [M/2](올림) - 1개의 키를 가져야 한다 (단, root node는 제외)
- 예를 들어, B-Tree의 차수가 3이면, 각 노드는 최대 2개의 키, 최소 1개의 키, 3개의 자식 포인터를 가질 수 있다
- 중간 노드의 key수가 x개라면 자식 노드는 언제나 x+1개가 된다 (항상 성립)
(아래 절에서 B-Tree의 데이터 삽입, 삭제를 보면서 다시 설명하겠습니다 - 실습이 이해가 잘되더라고요)

- 루트 노드는 하나의 노드로 이루어지지만 여러 정보를 담을 수 있어 전체 데이터 분포에 따라 균형을 유지할 수 있는 범위로 나눠서 저장하고 있다
하나의 노드에 여러 데이터정보를 저장한다는 것은 어떤 이점들을 가져올 수 있을까?
- 데이터베이스에서 데이터 조회는 결국 디스크 I/O이다 하나의 블럭에 최대한의 데이터를 저장해놓아야 한 번의 디스크 I/O로 많은 데이터를 읽어올 수 있으므로 성능에 좋다
데이터베이스 성능에 영향을 가장 크게 주는 요인이 랜덤 디스크 I/O이다 따라서 한 번의 디스크 I/O로 최대한의 데이터를 읽어와 메모리에 캐싱하여 사용할 수 있다면 탐색의 성능이 좋다
- 랜덤 디스크 I/O를 줄이고 선형 디스크 I/O의 방식으로 고안된 것이 B+Tree
정확히 이해하기 위해서 데이터베이스 관점에서 디스크 I/O와 저장 형태에 대해 이해가 필요하다
데이터베이스 관점에서의 디스크I/O
- 데이터베이스의 데이터는 Secondary Storage (SSD / HDD)에 저장된다
- 데이터베이스에서의 디스크 I/O는 이 Secondary Storage에 저장된 데이터를 블럭 단위로 읽어온다(블럭은 일반적으로 4, 8, 16KB 단위)
- 블럭 단위로 읽어온 데이터를 메인 메모리에 올려 저장한다
- 데이터 노드들이 각 블럭 단위가 되며 트리의 각 노드를 읽는 것은 디스크 I/O 1회라고 생각할 수 있음
- 트리의 깊이가 깊어질수록 디스크 I/O가 많이 발생한다는 의미
- B-Tree가 나온 이유도 여기서 찾을 수 있다
- 하나의 노드를 읽어오는데 블럭 단위이다 -> 노드의 값이 한 개이면 낭비되는 블럭 메모리가 존재 -> 하나의 노드에 여러 key값을 저장 -> 범위 탐색에 용이하며 트리의 깊이가 낮아지는 효과 -> 디스크 I/O 저하 -> 성능 향상
- 트리의 깊이가 깊어질수록 디스크 I/O가 많이 발생한다는 의미
성능을 올리려면?
- 데이터베이스에서 디스크 I/O를 통한 데이터 조회는 최대한 적게 접근하는 것이 좋음
- 메모리의 크기는 크지 않으니 최소한의 메모리에 필요한 정보를 담아서 올려야 성능 최적화가 가능
- 블럭 단위로 읽으니 연관된 데이터를 한쪽에 잘 모아서 저장하면 더 효율적으로 읽어올 수 있다
위 내용을 기억하고 직접 B-Tree에 데이터 삽입, 삭제를 해보면 왜 데이터베이스의 인덱스로 B-Tree 자료구조를 활용하는지 이해하기 쉬울 것이다
B-Tree 데이터 삽입
- 데이터 삽입은 항상 leaf 노드에서 이루어진다
- 노드에 key값이 초과되면 중간 키 값(정렬된 상태에서 중간 값)을 기준으로 좌 우 키들은 분할하고 가운데 키는 부모노드로 승진한다
M = 3인 경우로 테스트 (visualization 사이트)
- B-Tree의 차수가 3이면, 각 노드는 최대 2개의 키, 최소 1개의 키(root제외), 3개의 자식 포인터(root, leaf 제외)를 가질 수 있다
1. 1을 노드에 추가한다

2. 15를 추가 -> root 노드에 key값이 1개이므로 root 노드에 삽입 (M이 3이므로 최대 2개 가능)

3. 2를 추가 -> root 노드에 key값이 3개가 되므로 이를 분리해야 함
- 오름차순으로 정렬된 상태에서 분리가 이루어지므로 노드 데이터는 1-2-15
- 가운데 노드가 부모로 승진하고 두 노드가 분리되므로 root 노드는 2가 되고 자식으로 1과 15로 분리될 것

4. 5를 추가 -> root 노드 기준 왼쪽이 2보다 작고, 오른쪽이 2보다 크므로 오른쪽 진입 -> 15가 있는 노드의 key가 1개이므로 삽입

5. 30 추가 -> root 노드 기준 오른쪽으로 이동 -> key가 3개가 되므로 분리가 필요
- 정렬된 상태로 노드를 분리하므로 5-15-30의 형태
- 15가 부모로 승진하므로 루트가 2-15 오른쪽 자식은 5와 15로 분리
- root 노드의 key값 2보다 작은 1이 자식, 두 키 값 2와 15 사이의 5가 자식, 15보다 큰 30이 자식을 이루며 최대 자식 3개를 이루고 있음

6.90 추가 -> root 노드 기준 15보다 큰 쪽으로 이동 -> key가 1개이므로 30 옆에 삽입

7. 20 추가 -> root 노드 기준 15보다 큰 쪽으로 이동 -> key가 3개이므로 분리가 필요
- 정렬된 상태로 노드를 분리하므로 20-30-90의 형태
- 30이 부모로 승진
- 부모의 key가 3개가 됨 2-15-30의 형태이므로 분리가 필요
- 15가 root로 승진, 그 사이의 키 값 2와 30이 분리
- 20과 90이 30의 자식으로 분리됨
위 과정을 통해 자식이 3개 초과가 될 일이 존재할 수 없다는 것을 알 수 있다 (B Tree 규칙)
- 자식이 3개인 상태에서 key값이 초과되어 분리가 일어날 때
- 자식이 3개라는 것은 부모의 key값이 두 개라는 것이고 -> 자식에서 분리가 일어나 가운데 키 값이 부모로 승진한다는 것은 결국 부모도 쪼개질 것이라는 의미 -> 분리된다는 것은 자식이 나뉜다는 것

8. 7 추가 -> root 노드 기준 15보다 작은 왼쪽으로 이동 -> 2보다 큰 오른쪽으로 이동 -> leaf 노드의 키 값이 1개이므로 삽입

데이터 삽입은 위와 같은 규칙에 따라 이루어지는 것을 알 수 있다
B-Tree 데이터 삭제
- 삭제도 leaf 노드에서만 발생
- 삭제 후 최소 key 수 보다 적어진다면 재조정이 이루어진다
- key 수가 여유 있는 형제의 지원을 받는 방법
- 왼쪽 형제가 여유가 있다면
- 왼쪽 노드의 가장 큰 key를 부모 노드의 나와 형제 사이에 둔다 (1,2 - 3 - x였다면 가장 큰 수 2를 1 -2 - 3으로 변경)
- 원래 자리에 있던 key는 가장 왼쪽으로 이동시킨다
- 오른쪽 형제가 여유가 있다면
- 오른쪽 노드의 가장 작은 key를 부모 노드의 나와 형제 사이에 둔다
- 원래 자리에 있던 key는 나의 가장 오른쪽에 둔다
- 왼쪽 형제가 여유가 있다면
- 1번이 불가능하다면 부모의 지원을 받고 형제와 합침
- 왼쪽 형제가 있다면
- 왼쪽 형제와 나 사이의 key를 부모로부터 받아 데이터를 삭제하는 노드의 남은 키와 합쳐서 왼쪽 노드에 합친다
- 데이터를 삭제하는 노드가 비어있으므로 삭제한다
- 오른쪽 형제가 있다면
- 왼쪽 형제와 나 사이의 key를 부모로부터 받는다
- 왼쪽 형제의 key를 나한테 합친다
- 왼쪽 형제 노드는 비어있으므로 삭제한다
- 왼쪽 형제가 있다면
- 2번 후 부모에 문제가 있다면 다시 재조정
- 부모가 root 노드가 아니라면
- 부모 위치에서 1번 시나리오부터 재조정 작업을 한다
- 부모가 root 노드고 비어있다면
- 부모 노드를 삭제한다
- 직전에 합쳐진 노드가 root 노드가 된다
- 부모가 root 노드가 아니라면
- key 수가 여유 있는 형제의 지원을 받는 방법

1. 28 삭제 (1-1 시나리오)-> 삭제 후 key 수가 0개로 최소 키 보다 적은 노드가 발생 -> key수가 여유 있는 형제의 지원을 받는다
- 20과 22 중 하나를 지원받는데 큰 것을 지원받음
- 22를 부모 노드의 나와 왼쪽 노드 사이에 둔다
- 원래 부모노드에 있던 25를 가장 왼쪽에 key값을 둔다
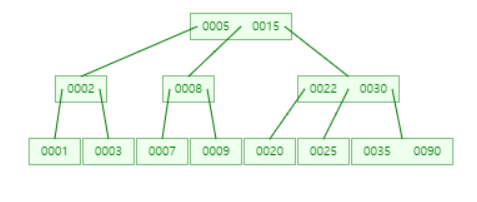
2. 25 삭제(1-2 시나리오) -> 삭제 후 key 수가 0개 -> 형제 노드의 지원을 받으려고 보니 왼쪽은 지원 불가, 오른쪽 형제의 지원을 받음
- 오른쪽 노드의 지원을 받으면 작은 key값을 지원받음
- 35를 부모 노드의 나와 오른쪽 사이에 둔다
- 원래 부모노드에 있던 30을 가장 오른쪽에 key값을 둔다

3 30 삭제 (2번 시나리오) -> 삭제 후 key수가 0개 -> 형제 노드도 key가 한 개여서 지원이 불가능 -> 부모의 지원을 받는다
-
- 왼쪽 형제가 존재하므로 부모 노드의 key를 받아 왼쪽형제에 나의 남은 key(0개)와 합친다

4. 22 삭제 -> 삭제 후 최소 키보다 적지 않고 leaf 노드이므로 그냥 삭제된다

5. 20 삭제 -> 형제의 도움을 받을 수 없다 -> 부모의 지원을 받는다
- 오른쪽 형제만 존재하므로 나와 오른쪽 형제 사이의 key를 받는다
- 삭제할 데이터가 존재하는 노드에 오른쪽 형제의 키와 부모에게 받은 키를 합친다
- 그런데, 부모의 키(35)를 주면서 부모 노드도 최소 키보다 적은 상황이 발생 -> 3번 시나리오에 해당 -> 마찬가지로 같은 원리가 적용됨 (root 노드가 아니므로)
- 형제노드의 도움을 받을 수 없음 -> 부모의 지원을 받음
- 왼쪽 노드와 나의 사이에 있는 키 15를 받아 왼쪽 노드에 합쳐진다

만약 leaf 노드가 아닌 중간에 위치한 노드가 삭제되는 경우
- leaf 노드에서 삭제하고 필요하면 재조정
- leaf 노드에 있는 데이터와 위치를 바꾼 후 삭제한다
leaf 노드에 있는 데이터 중 어떤 데이터와 위치를 바꿀지?
- 삭제할 데이터의 선임자나 후임자와 위치를 바꾼다
- 선임자: 나보다 작은 데이터들 중 가장 큰 데이터
- 후임자: 나보다 큰 데이터 중 가장 작은 데이터
선임자 후임자 선택은 어떤 데이터를 선택하는 것이 더 직관적이며 균형을 깨뜨리지 않을까를 고민해봐야 할 것 같다
데이터분포나 추후 들어올 데이터가 어떤 상태인지를 예측함에 따라 균형을 맞추는 비용이 더 적게 드는 쪽으로?..
위치를 변경하고 나면 위와 같은 규칙에 따라 삭제가 이루어진다
B*Tree, B+Tree
B*Tree의 경우는 B-Tree가 차수에 따라 키의 개수와 자식 노드의 개수를 컨트롤하고, 삽입, 삭제에 따른 균형을 맞추는 비용을 줄이고자 고안된 방식이다
- 노드의 추가적인 생성과 추가적인 연산의 최소화를 위해서 B-Tree에서 몇 가지 규칙이 추가된 B*Tree가 등장
B+Tree
B-Tree는 탐색을 위해 노드들을 이동하는 문제점이 있음
이러한 비용을 줄이기 위해 리프 노드에만 데이터를 존재시키고 중간 노드는 인덱스 노드로 활용
리프 노드에 존재하는 데이터들은 정렬되어있고, 각 노드들이 Linked List의 형태로 연결되어 있어 선형 탐색에 용이
MySQL의 DBMS는 B+Tree를 채택하여 사용하고 있음
정리
- 이진 탐색 트리는 불균형한 상태가 존재할 수 있어 탐색 비용이 최악의 경우 O(N)이다
- 균형 이진트리는 O(logN)을 보장하는 트리로 정렬 비용을 지불하고 탐색 성능을 올려주는 자료구조이다
- 데이터베이스는 Secondary Storage에 데이터를 저장하며 데이터를 읽어오기 위해서 디스크 I/O가 발생하고, 디스크 I/O의 횟수가 성능에 큰 영향을 준다
- B-Tree 인덱스는 균형이진트리에 비해 secondary storage 접근을 적게 한다
- B-Tree 노드는 블럭 단위의 저장 공간을 효율적으로 사용할 수 있다
- 균형이진트리의 노드들도 하나의 블럭안에 최대한 담는다면?
- 그게 결국 B Tree 동작 방식
- B-Tree에서의 데이터 삽입, 삭제 원리를 이해하면 정렬 비용, 데이터 분포가 중요한 이유를 알 수 있음
- Hash index를 쓰는 건?
- 삽입/삭제/조회의 시간 복잡도가 O(1)
- 같다 조회만 가능하고, 범위 기반 검색이나 정렬에는 사용될 수 없다는 단점이 있다
Reference
https://ssocoit.tistory.com/217#2.0_B*Tree_%ED%8A%B9%EC%A7%95
[자료구조] 간단히 알아보는 B-Tree, B+Tree, B*Tree
위 글을 보고 정리를 하지 않을 수 없었습니다. 가슴이 시키네요;; 그렇다면 바로 B-Tree, B*Tree, B+Tree의 특징에 대해서 알아봅시다. 목차 0. 이진트리 B-Tree, B*Tree, B+Tree에 대해서 알아보자면서 갑자
ssocoit.tistory.com
https://dataonair.or.kr/db-tech-reference/d-guide/sql/?mod=document&uid=360
데이터베이스 I/O 원리
4. 데이터 모델링의 3단계 진행 앞에서 라이브러리 캐시 최적화와 데이터베이스 Call 최소화를 통한 성능 개선 방법을 알아보았다. 본 절에서는 데이터베이스 I/O 효율화 및 버퍼캐시 최적화 방법
dataonair.or.kr
https://mangkyu.tistory.com/286
[MySQL] B-Tree로 인덱스(Index)에 대해 쉽고 완벽하게 이해하기
인덱스를 저장하는 방식(또는 알고리즘)에 따라 B-Tree 인덱스, Hash 인덱스, Fractal 인덱스 등으로 나눌 수 있습니다. 일반적으로 B-Tree 구조가 사용되기 때문에 B-Tree 인덱스를 통해 인덱스의 동작
mangkyu.tistory.com
https://www.cs.usfca.edu/~galles/visualization/BTree.html
B-Tree Visualization
www.cs.usfca.edu
'데이터베이스' 카테고리의 다른 글
| 테이블 조인 (1) | 2023.09.13 |
|---|---|
| 동시성 제어와 Snapshot Isolation (0) | 2023.09.11 |
| 트랜잭션 격리수준 (0) | 2023.09.09 |
| 트랜잭션 (0) | 2023.09.07 |
| 데이터베이스 반정규화 (1) | 2023.09.06 |


